📐 Measure of Shape

Last Updated: Jan 2026

---

Measure of Shape describes the shape of data distribution.

It tells us:

• Data kis taraf jhuk raha hai (skewness)
• Data kitna peaked ya flat hai (kurtosis)

🗣 Hinglish Tip: Shape = data ka overall pattern / curve ka nature

Shape helps to:

• Understand data distribution
• Choose correct statistical methods
• Analyze real-world datasets

Types of Measure of Shape

1. Skewness
2. Kurtosis

---

Skewness

Skewness measures the asymmetry of data distribution.

It shows whether data is:

• Symmetric
• Right-skewed
• Left-skewed

Formula Population Skewness

γ₁ = Σ(xᵢ − μ)³ / (N σ³)

Where:

• γ₁ = population skewness
• μ = population mean
• σ = population standard deviation
• N = population size

---

Sample Skewness

g₁ = Σ(xᵢ − x̄)³ / ((n − 1) s³)

🗣 Hinglish Tip: Tail jidhar lambi ho → skewness udhar hoti hai

---

Types of Skewness

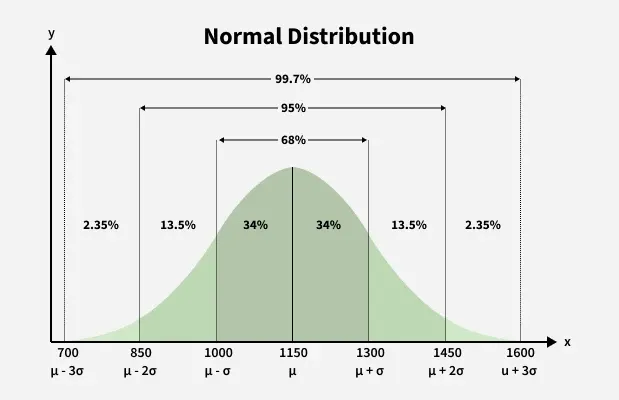
1.Symmetric/Normal Distribution

• Mean = Median = Mode
• Skewness = 0
• Bell shape curve

[]

---

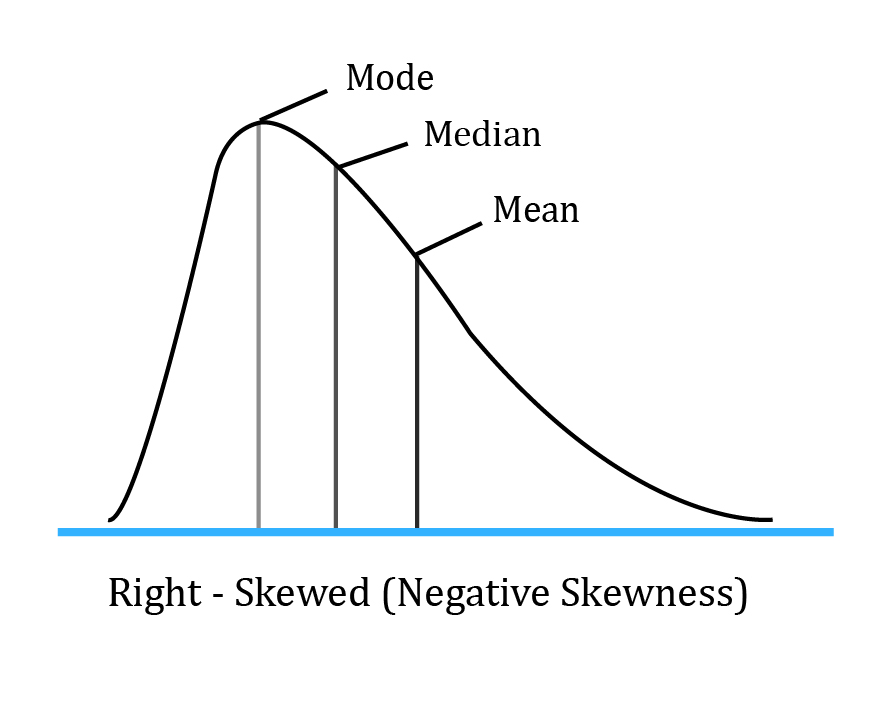
2.Right-skewed/Positive Skewness

• Mean > Median > Mode
• Skewness > 0

[]

---

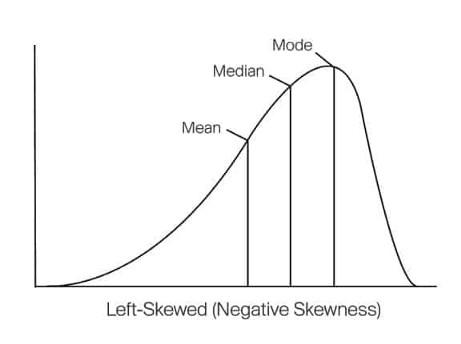
3.Left-skewed/Negative Skewness

• Mean < Median < Mode
• Skewness < 0

[]

---

Kurtosis

Kurtosis measures the peakedness or flatness of the distribution.

It focuses on:

• Height of the peak
• Weight of the tails

Formula Population Kurtosis

β₂ = Σ(xᵢ − μ)⁴ / (N σ⁴)

---

Excess Kurtosis

Excess Kurtosis = β₂ − 3

(3 is kurtosis of normal distribution)

---

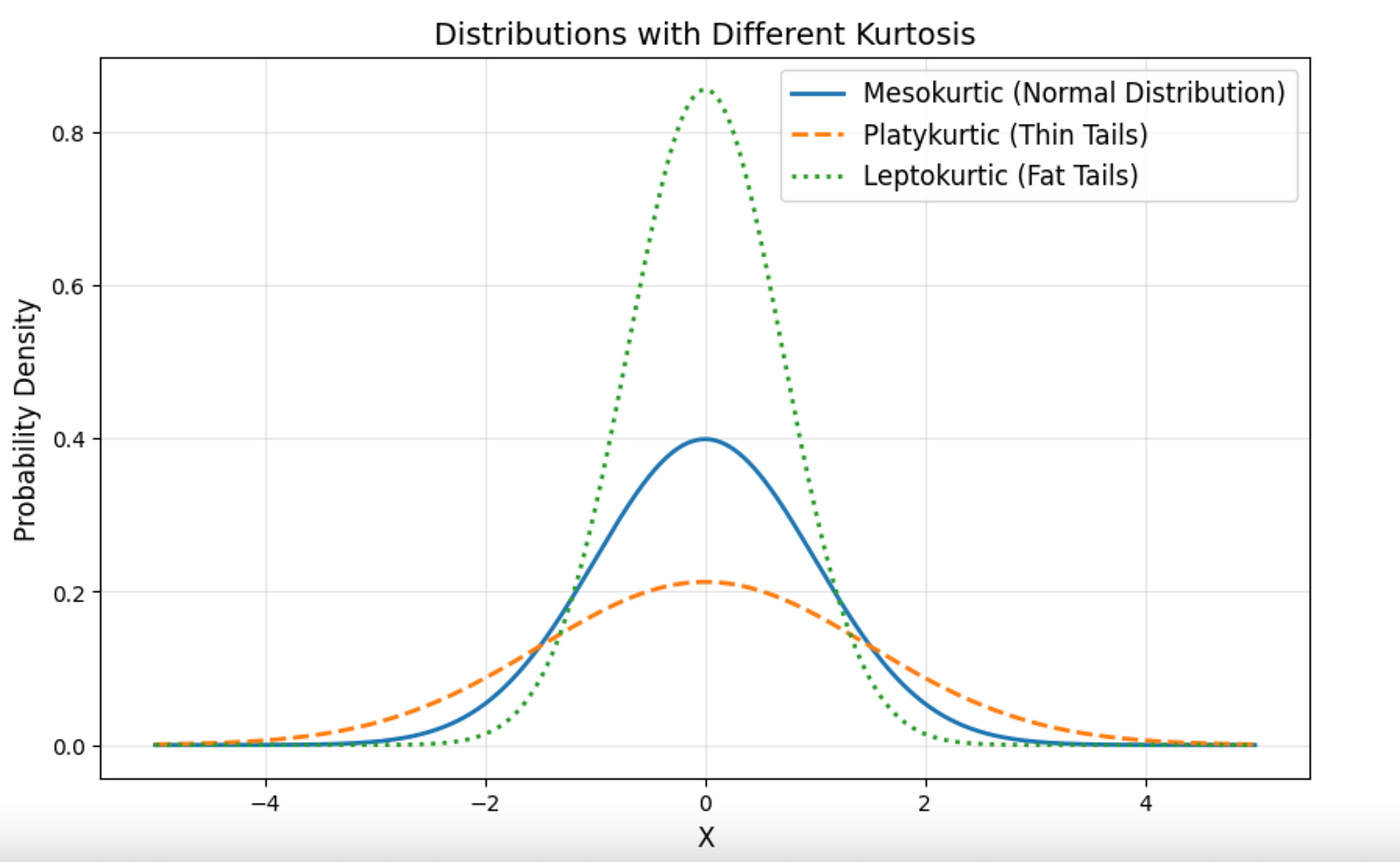
Types of Kurtosis

Kurtosis Type	Excess Kurtosis	Shape
Leptokurtic	> 0	Sharp peak, heavy tails
Mesokurtic	= 0	Normal distribution
Platykurtic	< 0	Flat peak, light tails

[]

🗣 Hinglish Tip: Kurtosis = curve kitni pointed ya flat hai

---